Today we will try to overclock a GF3 video card in artificially created frosty conditions.

But first of all I should give you the links to the articles which contain the whole theoretical base connected with this GPU:

• GPU NVIDIA GeForce3 and cards on it
• Optimization of NVIDIA GeForce3 for Intel Pentium4 and AMD Athlon
• MadOnion 3DMark2001 and NVIDIA GeForce3 - the love story
• NVIDIA GeForce3 benchmarking with Vulpine GLMark
• ASUS AGP-V8200 Deluxe - the following issues are concerned: anti-aliasing, scalability, operation in severe conditions (Giants, Aquanox, Quake3 (Maximum,Quaver))
• Leadtek WinFast GeForce3 - the following issues are concerned: anisotropy in Direct3D (3DMark2001), operation in severe conditions (GLMark) with time dependence of FPS introduced in graphs
• Gigabyte GV-GF3000D - the following issues are concerned: simultaneous activation of anisotropy and anti-aliasing, their complex effect on the performance (Quake3)

As you already know, the NVIDIA GeForce3 has a core frequency equal to 200 MHz and is equipped with a memory working at 230 (460) MHz. At the expense of its architecture, the video cards on this processor show an excellent speed in 32-bit color outscoring their competitors based on the GeForce2 Ultra, whose core works at 250 MHz.

Despite the 0.15 micron fab process of the GF3, this GPU has 57 million transistors and is very complicated in its architecture, and a large cache inside the chip lowers the potential in increasing the clock speed. But does it make sense to lift it? Yes, it does! In the articles above it is shown that with some functions enabled the performance falls by a great margin, especially in case of the simultaneous use of anisotropic filtering and anti-aliasing. That is why we are greatly concerned about the possibilities to increase the frequency, i.e. the speed of the chipset and the memory.

Let's open our refrigerator:

and see what's there... there we have a Athlon 1.2 GHz based system:

• AMD Athlon 1200 CPU (133 MHz x 9):
• Chaintech 7KJD (AMD760) mainboard;
• RAM 256 MBytes DDR SDRAM PC2100;
• Inno3D Tornado GeForce3 video card;
• HDD IBM DTLA 45 GBytes;
• OS Windows 98 SE;

  As you can see, we have chosen the Inno3D Tornado GeForce3 video card. It is based of the reference design, that is why it doesn't much differ from its brothers. We have already examined this card. Nevertheless, we have to work on it a bit more for making the overclocking process better:

For this purpose we used fine-grain emery paper. Look at the chipset and you will see that a metallic lid in its center is recessed, and plastic panels are towering above the center. Even if it makes less than a millimeter, heat emission gets worse since a heat sink rests against the panels. Heat between the lid and the heat sink can be transferred only through paste, but it is not very good. That is why we have decided to remove the difference between the panels of the chip and the lid with an emery. Now let's pop in the fridge to test the system at 18 degrees C below the zero.

Of course, we can also achieve excellent results using instead of a freezing room a Peltier element, for example. Let me show you such cooling system by the example of two video cards.

ASUS AGP-V8200 Deluxe

First of all I will show you a central heat sink having taken out black clips from it with which it is attached to the card.

We have prepared the clips for a new mount by cutting the spring which presses the heat sink to the card. All this is shown on the photos above. Then we have covered the chip with a thin layer of thermo-paste. And only after that we have installed the Peltier element (DO NOT MIX UP COOLING AND HEAT DISSIPATING SIDES!). You can see it on the photos below:

And then we have mounted a cooler (the distance from the heat sink to the card has become longer, that is why we have prepared the clips the above mentioned way):

But utilization of a regular cooler is not very effective, since the Peltier element dissipates a lot of heat, and such a low-fin heat sink is not capable of diffusing it. But we can go another way using coolers from other devices, for instance, from central processors. You can choose, for example, a massive cooler from the Intel Pentium III and mount it over the Peltier module:

On the upper right picture you can see how to mount this heat sink with the help of erasers and even with a single-conductor telephone cable.

Inno3D Tornado GeForce3

The mounting operations are similar to the above, that is why I will give you only the pictorial instructions:

Such a cooling method allows for raising the GPU frequency up to 250-270 MHz. It is less than the results obtained in the freezer. Besides, in case of the Peltier element we cool only the chip, while in the freezer we help the GPU and the memory as well. But the latter method is easier to implement.

Test results

For testing we used drivers from NVIDIA of 12.40 version, VSync was off. As a test application we used the id Software Quake3 v.1.17 - a game-test which demonstrates the card's operation in OpenGL with usage of a standard demo-benchmark demo002 and Quaver, that shows the video card performance at the Q3DM9 level with a great number of large textures.

Core and memory overclocking in Quake3, demo002

We took measurements in each 10 MHz step of the core frequency at the fixed minimal and maximum memory frequencies and vice versa. Such extreme overclocking in the freezing room helped us to achieve 300/295 (590) MHz!!!

So, let's look at the results in different resolutions.

• 1024x768


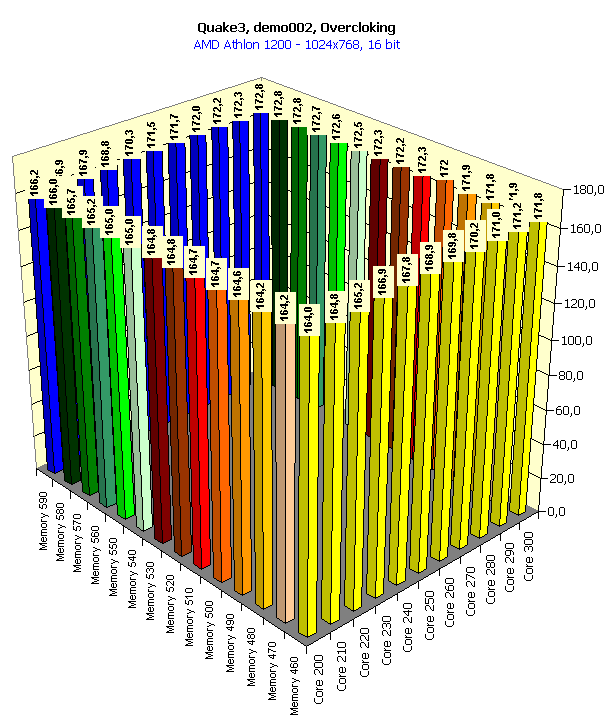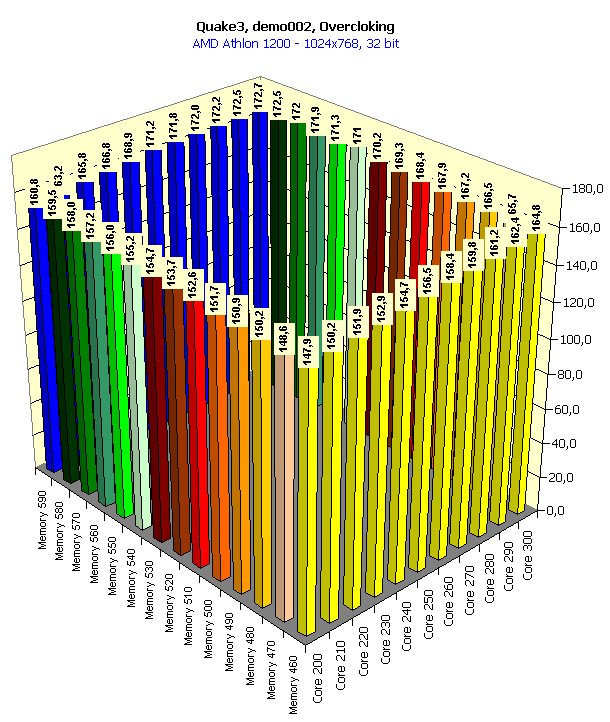In 16-bit color the overclocking doesn't help, the performance is limited by the CPU frequency. In 32-color the situation is almost the same.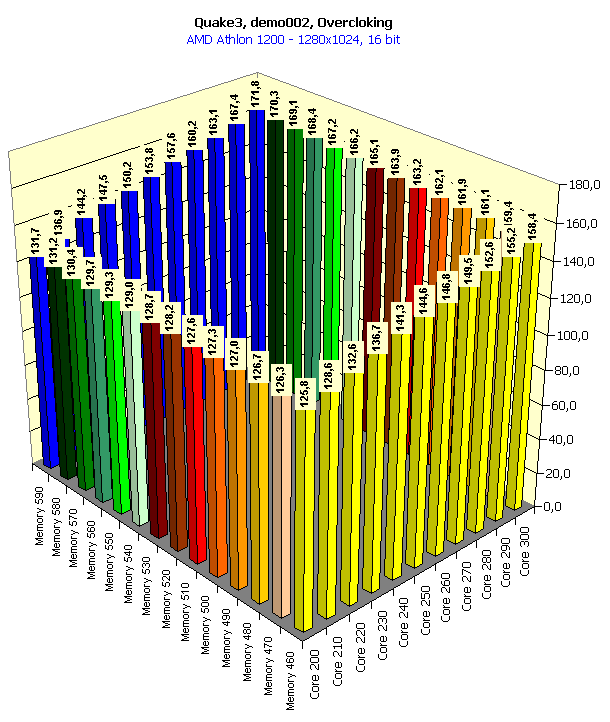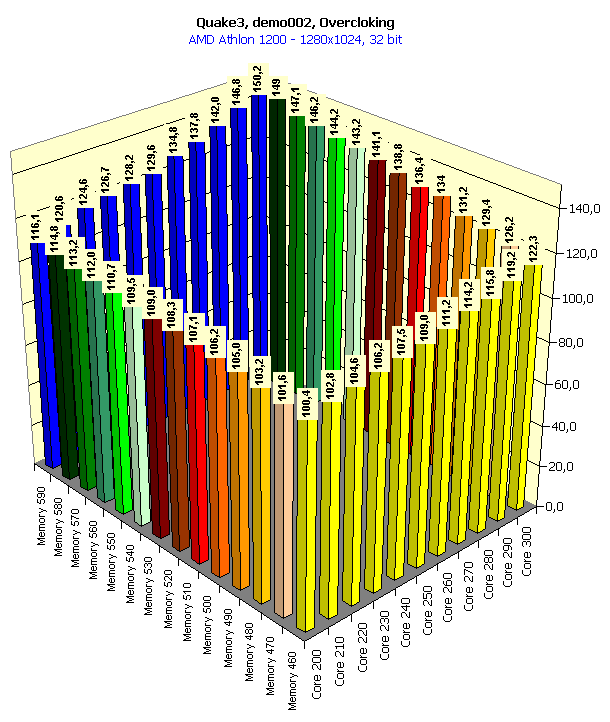

• 1280x1024


Here the accelerator makes a greater contribution, especially in 32-bit color. It is interesting that the raise of the core frequency gives a greater credit than a growth of the memory clock speed. In 16-bit color overclocking of the memory gives nearly nothing to the graphics processor working at 200 MHz. But an expand of the video memory bandwidth has a considerable effect on the overall performance for the 300-MHz chip. It implies, that GeForce3 cards are well balanced, and the 200 MHz GPU doesn't need a faster memory. Only with an increase of the core clock speed, especially when reaching the maximum value (300 MHz), the memory bandwidth is insufficient, and then an increase of its frequency makes a positive effect. In 32-bit color the memory frequency has a stronger effect since the volume pumped through the video memory raises, and the memory bandwidth becomes insufficient with a slight increase of the core frequency.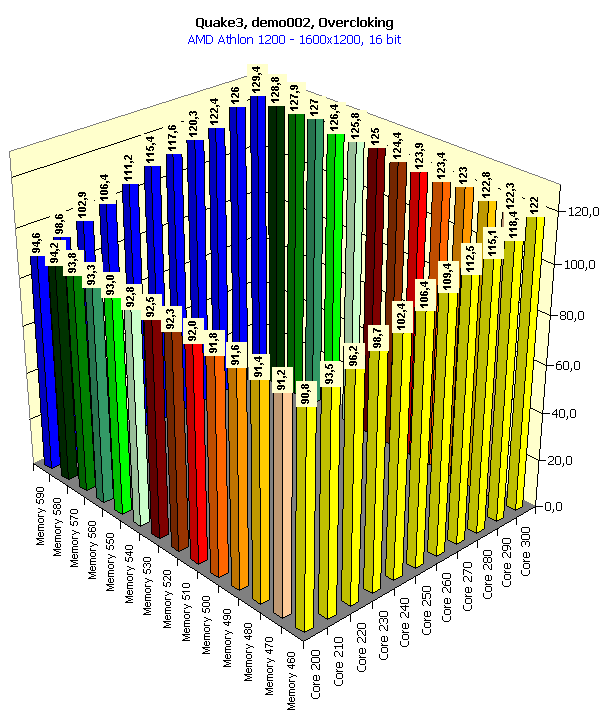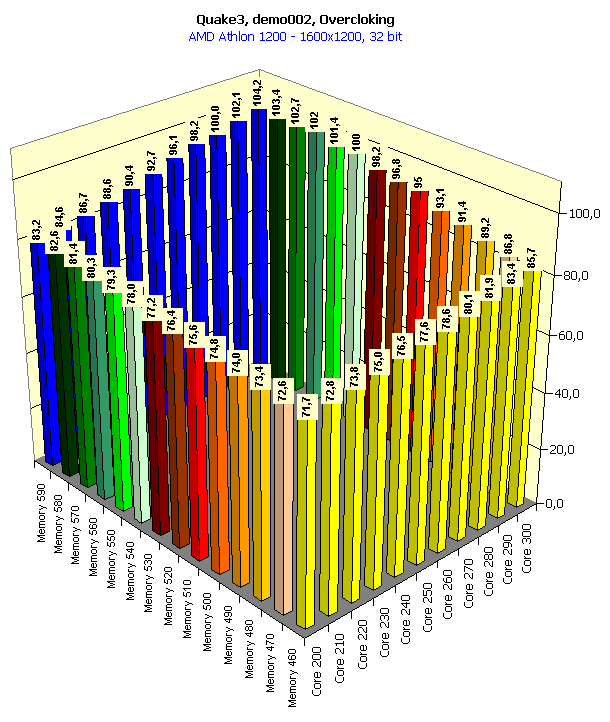

• 1600x1200


The situation is similar.

In conclusion of this part I should notice that if a card of the GeForce3 level with 300/295 (590) MHz frequencies appears on the market, even without additional enhancements of the architecture of this processor we will get more than 100 fps in 1600X1200X32, which gives an excellent playability in this high resolution.

Core and memory overclocking with activation of anisotropic filtering and anti-aliasing

In our articles we wrote that the anisotropic filtering function affected the performance badly, but at the same time it was the most effective as far as the quality of a 3D scene was concerned, especially its highest degree (Level 8 or 32-tap). The performance can drop 2.5-3 times! But all you know that it gives the most beautiful image (see 3Digest). And what if to add anti-aliasing? The GeForce3 demonstrates the playability at the lowest level. Let's see what overclocking can give us here:

1024x768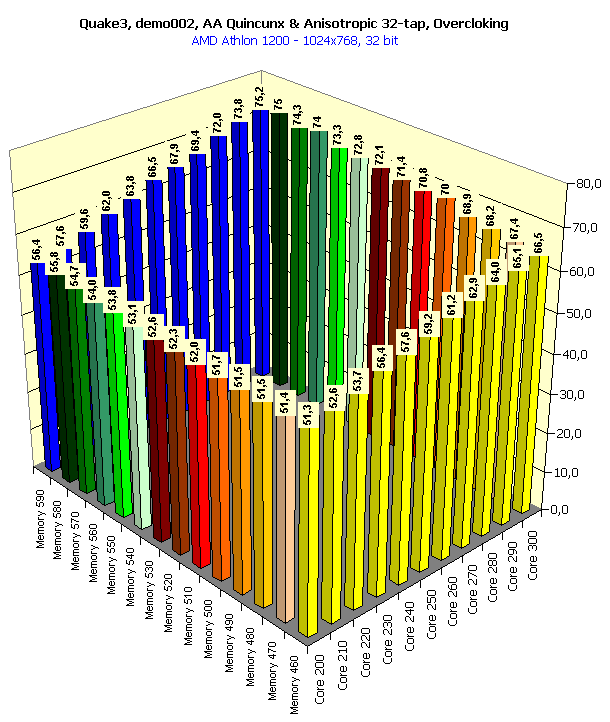

You can see that the overclocking allows for 47% performance boost! We have got 75 fps, and it gives an excellent playability in 1024X768 at 32-bit color. So, with an accelerator of the GeForce3 possibilities but which works at 300/295 (590) MHz there is no need anymore to think what a 3D function must be sacrificed to get better quality. We can easily play with the maximum anisotropic filtering and with Quincunx level AA enabled (which is the most optimal for the GeForce3).

Core and memory overclocking in Quake3, Quaver

This test was held at the maximum possible quality (the geometry and texture detailing was the best, trilinear filtering was used). It was interesting to look at the combination of the performance in 16- and 32-bit color with the separate overclocking of the core and the memory.

• 1024x768


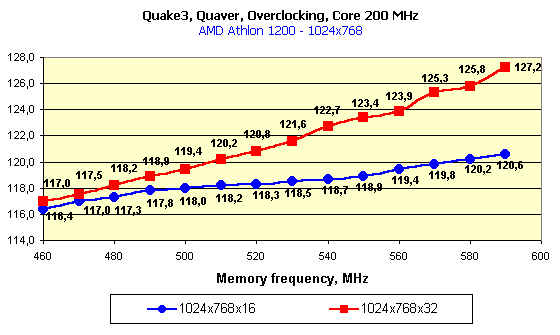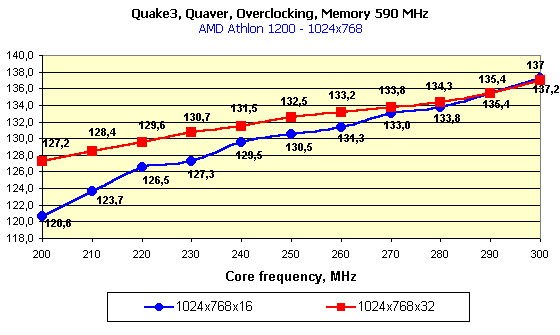At the definite frequencies the speed in 32-bit color is higher (!) than in 16-bit one. Look at the first diagram: at the rated frequencies the performances are nearly equal because of limitation by the processor frequency, but if we leave the core frequency at 200 MHz and lift the memory frequency, the gain in 32-bit color will be weightier than in 16-bit one. In this case (for the first time!) the video memory bandwidth is not anymore a bottleneck for the GPU potential. You all know that the GPU implements all calculations in 32-bit color and only at the determined 16-bit color it implements dithering decreasing the bit capacity of the color and the data volume which is to be pumped through the memory. At the expense of the latter the 16-bit color always won in speed. The more the memory bandwidth is limiting, the larger the gap between the performances in 16- and 32-bit colors.

Here the situation is different. The expenses for implementation of the dithering for 16-bit color are fatal! Operation in 32-bit color is beneficial from all standstills!

The second diagram shows what we can get if we will be gradually increasing the core frequency at the highest memory clock speed. At 200 MHz the 295 MHz memory is more than enough, but with the growth of the chip frequency it must be more demanding for the memory bandwidth. And we can see that only at the level of 280 MHz its performance in 16-bit color is nearly the same as that of the "trucolor", and it means that the 280 MHz GPU will be the best solution for the 295 MHz memory.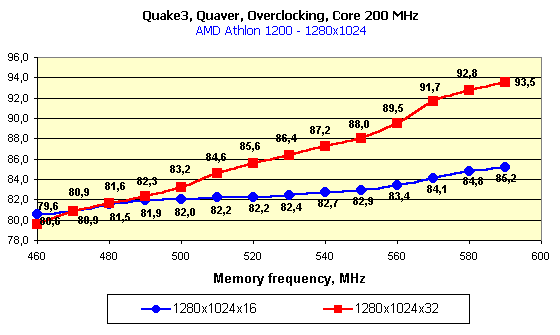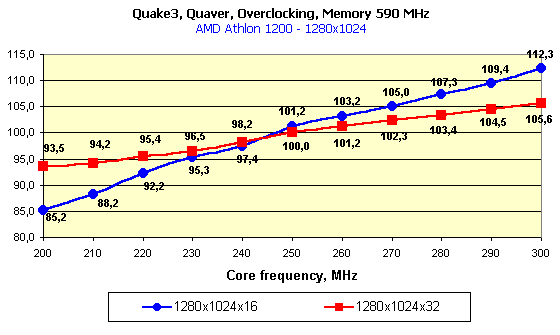

• 1280x1024


In 1280X1024 the combination of frequencies where the 32-bit color is an absolute leader takes place more seldom.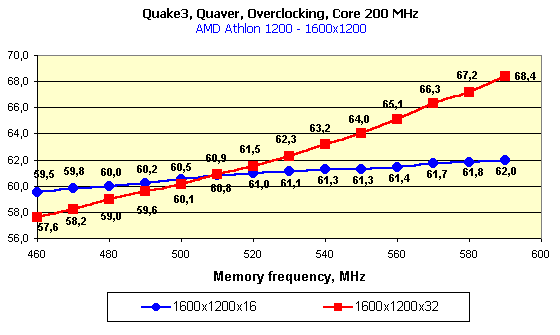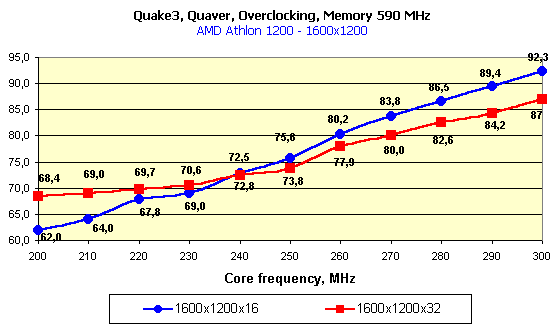

• 1600x1200

The trend keeps here, the operation in this resolution requires a larger memory bandwidth, that is why the 32-bit color outscores the 16-bit one only at the very high memory frequencies.

Conclusion

So, the experiment with placing the whole system block in the freezing room has given us the following interesting results:

An accelerator with an overclocked GeForce3 chipset (let it be produced according to the 0.13 micron technology) and with a very fast 300-MHz DDR memory would allows for:

1. excellent performance in all modern games in 1600X1200 at 32-bit color;
2. perfect playability in 1024X768 in 32-bit color with the anisotropy of the maximum degree and the Quincunx AA enabled (there is a choice: owners of large monitors can play in 1600X1200, others can play in 1024X768 with AA);
3. burying of 16-bit color.

That is why let's hope that the next baby of NVIDIA which is to be released at the end of autumn will give as all the above mentioned things. Besides, I don't exclude optimization of the architecture, integration of new interesting features allowing for lifting the 3D game quality and the speed in complex scenes.

Write a comment below. No registration needed!