As a physicist I must admit that in terms of mass speeds and energies a straight line can be considered as the shortest distance between two points. But on the other hand, I should admit that the most beautiful distance between two points is a curve, which should be smooth and at least of the third order. Undoubtedly, 3D models in the form of curves look more realistically than polygonal ones, especially if we closely look at them. By the way, a straight line is a parametric first order curve =).

Math-history

But at the standpoint of realization curves are not convenient. Why? First, let's consider a definition of curve. Let us assume that a curve (n is order) in a 3-dimensional space is specified as a variety of points (a trajectory) that can be unambiguously described the following way:

i.e. a set of three n order polynomials of some general variable (a parametrical value). So, with first power polynomials, we get a straight line, in case of the second power we get a quadratic (square) curve, in case of the third power, we get a cubic curve.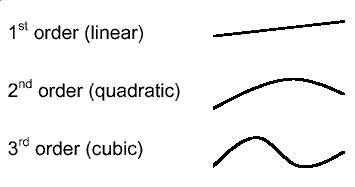

Higher order polynomials are rarely met, at least in the computer graphics.

So, having three n power polynomials we have to define 3*(n+1) coefficients in order to set a curve unambiguously. Since it is inconvenient to work with infinite curves, parameter t is usually set to correspond within the definite range (usually 0..1). Such curves are called bounded curves, or segments. It is inconvenient to store and process curves in the original form (through polynomials) - it is preferable to define them by a set of pixels in a space:

Therefore, it is necessary to have formulae to transform n+1 coordinates of a pixel into coefficients. First of all, the formulae must ensure univocal correspondence, and they must have smooth splicing (matching) of segments. Having taken some set of k pixels:

grouped them the following way:

and built segments out of each four, we get an unbroken and smooth summary curve. Such representation will allow us to manipulate data and describe different curves, plain and complex lines.

Now let's replace a curve with a surface, one variable t with two (u,v) and polynomials with a product of two ones of the definite power of these variables. In order to define such structure in a 3D space we need 3*(n+1)*(n+1) numbers, or (n+1) squared pixels. I.e. 16 points (grid 4*4) for a third order surface (bicubic). The prefix bi means that a surface is defined with cubic polynomials according to each of two parameters.

In case of bicubic surfaces we can find such transform that would allows us not only to define clearly but also smoothly splice segments. These transforms are called B-Spline, Bezier Surfaces. A set of pixels and parameters is called Patch.

From theory to practice

Everything described above requires a heap of calculations. The worst is drawing of segments. While for a triangle we can swiftly build univocal correspondence of a screen pixel and a texture/lighting parameters and shade it quickly with incremental algorithms, second and third power surfaces are much more difficult to draw. First, it is impossible to find univocal correspondence between a pixel on a screen and a point on a surface since an equation of the order higher than 1 can have different number of solutions or even doesn't have them. I.e. in case of a bicubic surface up to 3 points of the surface can pretend to one screen pixel. And to find the right solutions is computationally expensive. That is why it was decided to divide a surface segment with an even grid, calculate intermediate points and draw a surface as a set of triangles based on these points. This process is called tessellation - partitioning of a higher order primitive into a set of lower order primitives (in our case they are triangles). Earlier such operations were carried out by processors and applications, now they are gradually transmitting to the level of drivers, accelerators and API: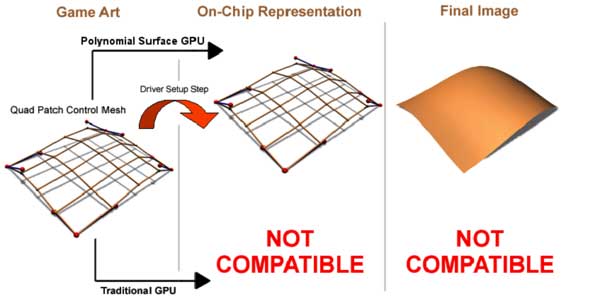

for example, NVIDIA GeForce3 can tessellate rectangular patches on a hardware level, and this possibility is supported in the DirectX 8.

Highs:

1. In case of the hardware tessellation the AGP and the memory bus are not loaded so significantly - we store and transfer a small number of geometrical information, and as a result we get a detailed surface made of a great deal of triangles.
2. It is easy to draw models defined by such a way with an adaptive (depending on the distance to a model) detailing level - we just change the number of triangles into which the segment is divided by an accelerator.
3. We use up the power of modern accelerators and, first of all, their T&L blocks, without being limited by a weak CPU of the system.
4. A great deal of triangles allow us to realize lighting and shadows without light maps making shaders and T&L responsible for it. Such approach means a dynamical media - all objects will cast shadows, all light sources will be moving according to arbitrary trajectories. A necessity in long preliminary calculations will disappear.

Lows:

1. There will be a necessity, in fact, in two versions of description of the world and models in a game - defined in the form of curves for accelerators that don't support hardware tessellation, and in the form of straight lines for those that don't support it. In the DirectX 8 a program emulation of this function is not available.
2. It is impossible to rework the already written software targeted at triangles.
3. Creation and editing of models built of such surfaces is not very convenient and elaborated as it is in a classical case.

At present, lows are outweighing the advantages, and at the first place is a commercial issue - no one is hurrying now to create and sell a game suitable only for the GeForce3.

True forms

Soon a competitor of the GeForce3 will appear on the market - it is a chip of a new generation from ATI codenamed R200. To hope for something ATI must offer a solution that will be technologically more perfect than that of NVIDIA. The only performance is not a determining factor. It means that not only shaders, multisampling and 3D textures are necessary, there must be something unique to help win the race. And ATI has developed a new technology called "TRUFORM". The technology is based on a new representation and a tessellation method of smooth surfaces, so called N-Patches. All this is supported on a hardware level in the R200: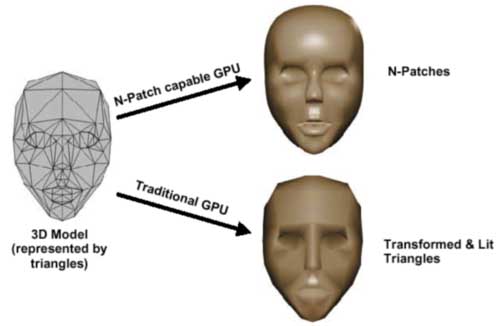

Let's look at the scheme in order to define the difference from the earlier described rectangular patches: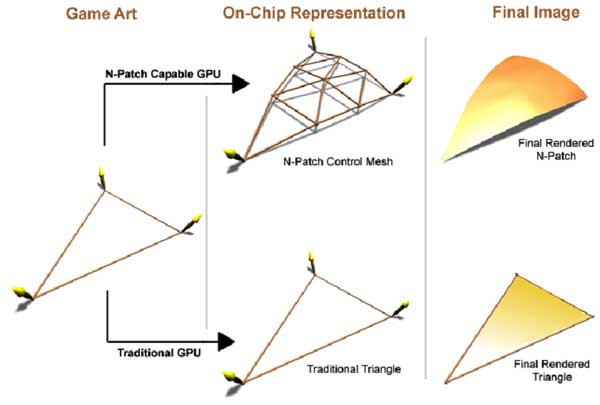

A new tessellation algorithm divides not a rectangular surface but a triangle into a regulated number of triangles with a predetermined normal vector for each point.

In order this polygonal model, passed through such tesselator, remained smooth it is necessary to provide matching of edges of each triangle of surfaces. Thus, a curve of an edge must be completely defined only by coordinates of limiting points and corresponding values of a normal. Let's look at how triangles are divided and how edges are matched. For each vertices of a triangle two control points are built (according to the number of adjacent sides). Either is calculated the following way: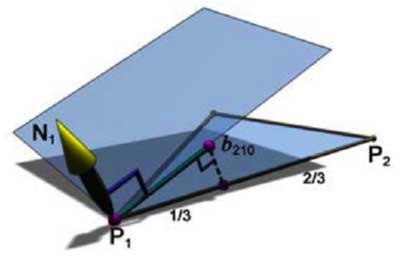

N1 - normal vector, P1 - vertex, the obtained control point b210 relates to P1 point and P1-P2 edge. The point lies at the intersection of a plane passing through the vertex athwart to the normal and through the edge parallel to the normal at the distance of one third of the edge's length. After calculation of one central control point we get the following set (10 points including vertices):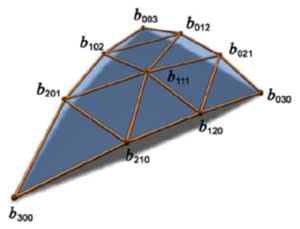

It should be noted that an average control point is calculated another way. After that, a smooth surface defined by these control points is tessellated up to the required level of smoothness. So, edges are matched, and the model becomes smoother with increasing a tessellation level: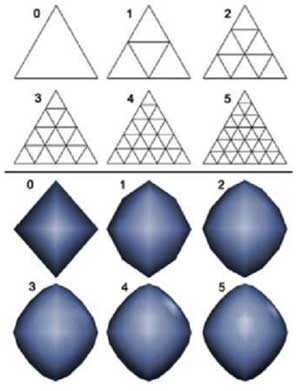

Remember that we also need to calculate coordinates of normals for more points. They are obtained by linear interpolation of the normals of the source vertices. For example, for the weakest partitioning, where we get 4 triangles instead of one, we can see the following picture: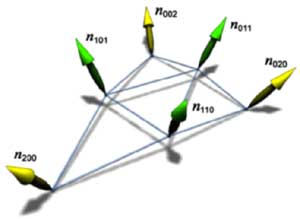

A normal vector of a point newly created on an edge is just a half-sum of vectors of vertices of the corresponding plane. Of course, this method of interpolation suits not only normals, but also all attributes of vertices, for example, coordinates of texture binding or color, transparency values, fog etc. Besides, the R200 offers a mode of advanced quality, where interpolation of channels is more complex, but the result is more accurate for a geometrical curvature of surface. It means that a grid, according to which parameters are interpolated linearly, contains trice more triangles than to be drawn. For each triangle drawn after tessellation intermediate values of parameters are found in the middle of its sides, and linear interpolation is implemented between them and vertices.

Let's look at the results of application of this technology to the geometry of a well-known model from DX8 SDK:

The results are clear. The most important is that a format of defining models hasn't changed! What we need is an old model defined through triangles, and normal vectors in each point will be defined with the required tessellation depth. At the programming standpoint, a code of drawing will remain the same - it is sufficient to once initialize usage of N-patches, set a tessellation depth and transfer triangles for drawing by a standard way, watching how they are turning into smooth surfaces.

But there is a pitfall. For calculation of lighting many applications use not normal vectors but light maps and other techniques delivering precalculated color values for vertices. In this case a perfect results will be ensured only for the geometry, but not for shading and texturing. Only those applications will get real advantages which are working with standard light sources and T&L possibilities - they need slight changes to support the new technology. Forcing of N-Patches at the drivers' level is also theoretically possible (for programs created earlier and "knowing" about this technology), but the decent results will be obtained in case of simple scenes with usage of a standard lighting model with defining of normals and light sources. It is possible that games with complicated multipass construction of scenes (e.g. Unreal) that use procedure textures and light maps won't be playable in such forced mode due to a great deal of different visual artifacts.

At present, the N-Patches technology is supported in the DirectX 8 and in the proprietary OpenGL extension that belongs to ATI. That is, it is available in all main APIs. The hardware support now is realized only in the R200.

Conclusion

All above mentioned highs of defining models in the form of curved surfaces relate to the TRUFORM technology. Here they are:

1. In case of the hardware realization of tessellation the AGP and memory bus are not unloaded - we store and transfer a small number of geometrical information, and receive a detailed surface made of a great deal of triangles.
2. It is easy to draw models defined by such a way with an adaptive (depending on the distance to a model) detailing level - we just change the number of triangles, into which the segment is divided by an accelerator.
3. We use up the power of modern accelerators and, first of all, their T&L blocks, without being limited by a weak CPU of the system.
4. A great deal of triangles allow us to realize lighting and shadows without light maps making shaders and T&L responsible for it. Such approach means that all objects will cast shadows, all light sources will be moving according to arbitrary trajectories. A necessity in long preliminary calculations will disappear.

   At the same time, triangular segments (N-Patches) used in the TRUFORM technologiy save us from all earlier mentioned drawbacks. And some of them even turn into advantages:

5. All models are defined by a single method regardless of whether this technology is supported on a hardware level. It means that art games don't need rework or special conditions for developing.
6. A code modification necessary for support of this technology is minimal. The code of drawing as a rule remains untapped, you are only to enable and disable the corresponding possibility in time.
7. A potential possibility of forcing this technology on the drivers' level (undecided)
8. DirectX 8 and OpenGL support

So, let's wait for the first R200 based cards and see how the TRUFORM will work.

Write a comment below. No registration needed!